Sample MM Lesson Plan
Contents
Oregon Curriculum Network: A Digital Mathematics
Sample Lesson Plan (Martian Math)
Playing With Blocks
|
BackgroundPlane nets typically come with mathematical expressions, other mathematical information, giving the dimensions of these nets with precise measurements. This would be in contrast to topological networks or graphs, wherein the connections matter (which dots connect to which other dots), but not the edge lengths. Do we care about knots? The plane nets in this lesson plan all correspond to convex polyhedra, tetrahedra in particular, although these tetrahedra are used to assemble other shapes. When the plane net contains an unknown h in all edges, this suggests an ability to rescale, which results in changes to volume as a third power of changes to edge length. Our work with these tetrahedral modules (Martian imports) reminds us of these rules. MaterialsNo matter what your local construction material, perhaps paper, perhaps imaginary and/or computer generated, consider metal stamping and folding a possible topic. How are car bodies made? Watch some YouTubes or listen to machinists describe their metal work. Does your school have its own metal working shop or perhaps sources of clay? Paper is not the only option. You may wish to recycle already manufactured parts in some lessons, not construct from raw materials.
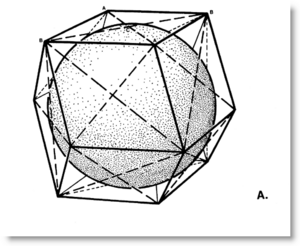
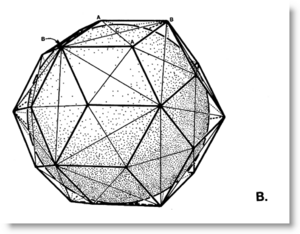
WorkflowA factory line approach may be adopted where your students change roles, as cutters, folders, tapers, construction site assemblers. You need a stream of left and right handed versions, a place to build inventory. Building a regular tetrahedron and octahedron from these modules should be a fun and engaging process, instructive and sociable. Those wishing to run the whole process alone will have done each job in sequence, so will have all the skills necessary to complete the job as home work. Optional: build Couplers from MITEs and emphasize the common twenty-four count in the regular tetrahedron and coupler, which have the same volume. The rhombic dodecahedron, of twelve half-couplers, weighs in at volume six (144 modules). Remember: A MITE is a MInimum space-filling TEtrahedron. The rhombic triacontahedron makes a fine ornament in any classroom. The fine line difference between a T and E module, and how this connects to the state standards power law, is a key topic for discussion. The rhombic triacontahedron of volume 5 has 120 T modules of the same volume as both the A and B modules. If you scale up the volume by 3/2, to 7.5, then your face center radius will be phi over sqrt(2). Other lesson plans branch off from here. |
|