Martian Math
Oregon Curriculum Network: A Digital Mathematics
Welcome to Mars
Martian Math is one of four nodes comprising an overview of a digital mathematics curriculum offered through Oregon Curriculum Network and, as such, are "tip of the iceberg summaries" not exhaustive presentations. Looking for an example lesson plan?. Example course?.
Martian Math or ET Math is a marketing wrapper around some futuristic math topics. For example: here's some recent Science News about the Tetrahedron.
In adding more eye candy and portraying the material as originating extra-terrestrially, we're taking advantage of a vast literature and shared images, from cartoons to science fiction movies.
These open resources also constitute an invitation to teachers to craft additional lesson plans making use of this framework as a basis for collaboration.
| Martian Math may be integrated into a four part curriculum as one of those parts, the other three being Neolithic Math, Supermarket Math and Casino Math. However, there's no reason one cannot separate these as relatively standalone curricula under the umbrella of discrete math (or "digital math" in some circles). | Note to Teachers: you may wish to localize your approach, connoting "from over the horizon" with a different set of metaphors. Most astronomy savvy students already know that Mars is in no position to be exporting math to contemporary Earthians. So if the plan is to stay more factual, feel free to suggest other images. Consider ETs from beyond the solar system, where additional water-rich planets like this one are predicted to occur. |
A word about jargon: you will find some familiar and unfamiliar abbreviations in Martian Math.
Q: What's this "CCP"?
Here's what Martians learn...
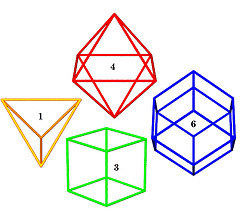
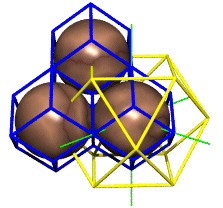
- a basic scaffolding or lattice dividing space into a pattern of cells or voids (containers). The XYZ scaffolding is perhaps the most familiar and consists exclusively of cubes. Less familiar to most students perhaps, is the scaffolding associated with the CCP, a sphere packing arrangement familiar to chemists and crystallographers, as well as to any vendor of hard spherical objects of quasi-uniform radius, such as fruit sellers, cannon or bowling ball vendors.
- a way of packing polyhedra into the CCP-based scaffolding, used by inventors Alexander Graham Bell (kites) and R. Buckminster Fuller (octet-truss), along with a large peer group in the architectural professions, including in space station design.
- ways of unpacking these polyhedra into smaller subunits or modules, another pass at the concept of space-filling, either by identical shapes or complementary shapes. For example, the regular tetrahedron and octahedron, of relative volume 1:4 and relative occurrence 2:1 (twice as many tetrahedra) comprise the CCP-based scaffolding we introduced under the first bullet point.
- ways of thinking about (designing, deploying, recycling) geodesic spheres and domes (yes Mars has lots of those, as well as Biosphere 2 looking buildings).
Note to Teachers: whereas these are all traditional topics with a long legacy, given our marketing wrapper (Martian Math), we're going to be using a somewhat alien-seeming nomenclature, albeit a well-designed and non-time-wasting one. However, the familiar ancient greek heritage will get into the mix, with vocabulary words such as icosahedron and rhombic dodecahedron.
Develop Skills
Mathematics is a hands-on subject on Mars, meaning that as students of this subject, you will have ample opportunity to grapple with tools of the trade, such as professional quality programming languages, ray tracers, physics engines and so forth.
Some segments will mention the Model View Controller design pattern, as a way of sorting some of our tools into categories.
- Model: simulations of how something works
- View: displays information about a model's state
- Controller: interacts with the model, selects views
In order to demonstrate your skills, to yourself and your audience, you will want to edit some of your output in the form of embeddable picture, sound and video formats, formats with special markups or control characters. These are tools of the trade in computer world. Whether you're planning to be a professional cartoonist, or still picture photographer, you will likely have need of skills related to the production, manipulation and storage of various standard types of media.
Among the quality program languages we plan to feature is Python. If you're thinking Mars has no pythons, think again.
Note to teachers: if your students think Martians are lame, don't enjoy that literature, feel free to consider citing grays under the Denver Airport as your source (allusions to mythological comic book and cartoon characters). Or use your imagination and develop some new lore.
Topics
So really, what is so different about Martian Math? Is this all phony fluff, carnival cotton candy for the mind? No way!
Actually, we do have a rather primitive difference to introduce, which is to knock the cube from its throne as somehow primary to other shapes, as the gridmeister. Our vocabulary registers the cube's setting of standards. The 90 degree angle is considered "normal" and to turn a 90 degree corner is to access a whole new dimension, going from width, say, to breadth.
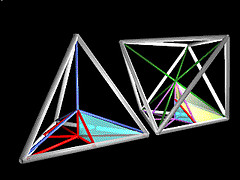
So what do Martians use in place of the Earthling cube? Why the tetrahedron of course, the simplest enclosure one might make with sticks, a cage of four windows, four corners, and six rods. This is our minimum tent and we float it in zero gravity space, or under the ocean's surface, to make the point that none of the four facets is "special" in being a "base" (an unnecessary complication, though we may well define a "base face" on a second or third pass through this topic).
To make a long story short, Martian Math uses a tetrahedron as its unit of volume. You will not find that in many textbooks as of 2009, when this preamble was first entered. Hence this "ET math" branding is actually somewhat apropos. You may really find yourself phoning home with this stuff, as your Earthling peers just won't know what page you're on, unless you share about this WikiEducator page on Martian Math.
Note to teachers: if you are well-versed in the history of ideas, including up through the 20th century, you have by now recognized our indebtedness to Bucky Fuller for a lot our shop talk and concepts.
Basic Scaffolding
When you fill a snugly fitting triangular rack with equi-diameter balls, and before you remove this rack, you have the option to pile a second layer of balls on the first. Because the rack is in place, the base does not spread much. Apply a third layer, and a fourth, until you reach an apex. You have built a tetrahedron. This is not a new trick, has been applied since time immemorial to stack anything roughly the same size and round e.g. fruit.
Actually, when you stare at a matrix of closest packed balls, such that the aerial view is of equilateral triangles wheeled around in hexagons, you're also staring at valleys between those balls. With a square matrix of balls, providing a grid of squares instead of triangles, you likewise have valleys, and relatively fewer in number. A second square of balls, with a ball count one less along each edge, fits snugly over the first. Each layer building towards an apex will consist of (N-1)(N-1) balls relative (N)(N) balls in the previous layer. Exhibit: original web page from Synergetics on the Web.
Packing Polyhedra
Unit of Volume
Four closest packed balls, each inter-tangent to three others, define with their four respective centers, the four corners of our unit of volume. The edges are each one sphere diameter in length. As these lengths extend, preserving aspect ratios, the surface area multiplies as a 2nd power of the linear scale factor, the volume as a 3rd power. We need not convert to square and cubic units however. Tetrahedra continue to provide our most primitive system of units, starting with the regular tetrahedron just described.
3,4-Fold SymmetryTwo intersecting tetrahedra, with edges crossing at 90 degrees, form the eight corners of a cube. Relative to our Martian unit, its volume is three. The octahedron formed by a square of balls, abetting from both sides by polar balls, has a relative volume of four. The rhombic dodecahedra around each ball, serving to encase each in a space-filling diamond-faceted capsule, each have a volume of six. Around every ball in our matrix (the CCP), twelve are in inter-tangency, at the corners of our volume twenty cuboctahedron. 5-Fold SymmetryThese lattice polyhedra interpenetrate the CCP spheres in a regularly repeating pattern. How to introduce five-fold symmetric polyhedra into this mix is a topic you'll hear the Martians talking about amongst themselves. Learn more Martian, why not? Unpacking Polyhedra
The cubic closest packing (CCP) defines a scaffolding or skeletal framework consisting of regular tetrahedral and octahedral volumes. These may be in turn dissected into irregular tetrahedra we label the A and the B, both occurring in left and right handed versions. The angles and edges of these component tetrahedra are available on-line, with plane nets available for downloading and folding. These plane nets may also be derived from scratch for exercise, if your course is sufficiently detailed and/or your students have the requisite mathematical maturity. The five-fold rotationally symmetric rhombic triacontahedron wraps a unit-radius CCP sphere with its 30 diamond-shaped facets (its rhombs). Said triacontahedron fits into our Martian concentric hierarchy at several points, volume-wise, including at values 5 and 7.5 (remember these are tetravolumes i.e. Martians have tetrahedral units of volume). The 120 T-modules defining the volume 5 rhombic triacontahedron each have a volume of 1/24. This is equivalent to the volume of two others, the A-module and B-module. These latter two will assemble all the aforementioned lattice polyhedra, such as the tetrahedron (volume 1), cube (volume 3), octahedron (volume 4), rhombic dodecahedron (volume 6) and cuboctahedron (volume 20).
Geodesic Spheres and DomesThe key bit of information here is that the cuboctahedral number sequence 1, 12, 42, 92... (expressible as a Python generator), is likewise the icosahedral number sequence. The ratio 1:2:3 for N:F:E where N = V - 2, V + F = E + 2, for omni-triangular geodesic spheres will be tested as basic to this curriculum, so watch for those story problems that require it. Links to virus morphology and buckminsterfullerene will be likewise somewhat de rigueur. InvestigationsInvestigations tend to be somewhat open ended and might be tackled at a variety of levels. Those listed below will suggest others and so forth, as students become oriented to finding their own way, in the context of whatever real world circumstances. Having one or more computer languages at one's elbow, such as Mathematica, Python or J, will provide additional opportunities for explorations and skills development. Note to teachers: there's plenty of room to create new WikiEducator pages providing your findings as a result of pursuing these and related investigations into Martian Mathematics. Produce your own content, build a portfolio, help us share in your love of learning. Waterman PolyhedraGiven the CCP, choose any ball as your origin. Connect this origin to some distal CCP ball center and call this your sweep out radius for a given Waterman Polyhedron. Every CCP ball at this radius will be a vertex of your polyhedron, however so will be every ball of lesser distance from the origin comprising the unique convex hull associated with this maximum upper limit. In other words, a Waterman Polyhedron's vertices include all CCP balls less than the limit distance from the origin that tend to make it more spherical. A literature has developed on this class of polyhedra, along with Java applets, ray tracings, algorithms. The open source Qhull code base might be pressed into service. Robert Gray proved the class of Watermans as described above all have whole number volumes relative to our unit volume tetrahedron of four CCP spheres. Link to LCD triangles. TensegrityThe tensegrity genre was realized in sculpture by the world renowned artist Kenneth Snelson, who attended the famed Black Mountain College contemporaneously with a favorite Martian. On computer, the rise of Elastic Interval Geometry garnered some attention among modelers, various brands of artist. Mathematically, an EIG engine iteratively evaluates vector sums as defined by a graph of edge-connected nodes, and where these edges have elastic properties (like springs). Enhancing student knowledge of vector graphics might be one motive for diving into this Martian machinery, seeing what makes it tick. See also: Flextegrity. Computational GeometryGeodesic spheres and domes are not difficult to construct, and yet one has a vast array of options as to what strategies and materials to employ. Start with the full sphere and understand the symmetries involved, the relationship between cuboctahedral and icosahedral packings, the sets of LCD triangles. SNEC has a track record of providing workshops, in cahoots with SUNY. Shop around for what's available in your area. Take advantage of what's already open source. Recycle. NanotechnologyBuckyballs and buckytubes provide an entryway into the world of nano-sized phenomena, as does virus morphology. Investigate cutting edge research by learning the namespaces, the technical shop talks used by specialists in this kind of research, especially Martians with their Mites, Sytes and Kites. Martians have been engaged in nanotechnology projects for a long time, so there's lots to learn here. Investigate the geometry of hexapents (e.g. the soccer ball), which occur naturally as well as artificially. |